Extras din curs
1. Noţiuni introductive
Lucrarea de faţă abordează problematica mijloacelor şi metodelor de
generare, transformare, amplificare şi memorare a impulsurilor electrice.
Circuitele de impulsuri sunt formate din surse, receptoare şi conexiunile
dinte ele. Receptoarele sunt constituite din elemente pasive de circuit (rezistenţe,
condensatoare, bobine, transformatoare) şi din elemente active (diode,
tranzistoare şi structuri integrate).
Prin impuls electric vom înţelege o tensiune variabilă (sau un curent
variabil), având intervalul de timp dintre două treceri succesive prin aceiaşi
valoare, mai mic sau comparabil cu durata regimului tranzitoriu al circuitului prin
care se transmite. Mărimea electrică aplicată la intrarea unui circuit se numeşte
semnal de intrare sau excitaţie iar cea obţinută la ieşire se numeşte semnal de
ieşire sau răspuns.
Un impuls este definit de parametrii descrişi în figura 1.1. unde
E - amplitudine
ti - durata impulsului (puls width)
tr - timp de creştere (rise time)
tf - timp de cădere (fall time)
V
E
τ1
semnal
treaptă
semnal liniar
variabil
semnal
exponenţial
t
t
ti t
kt
α = arctg k
Ui = E(1-e-t/τ1)
Figura 1.2. Semnale electrice
elementare
E
0,9E
0,1E
0,5E
y(t)
t t
tr
ti
tf (tc)
t
Figura 1.1. Impuls electric
Circuite numerice
2
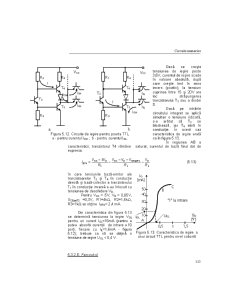
Impulsurile reale care apar în aplicaţiile practice pot fi exprimate prin
sume algebrice de semnale elementare. Semnalele elementare (figura 1.2) pot fi
semnale treaptă (caracterizate de amplitudinea E), semnale liniar variabile
(caracterizate de panta k) sau semnale exponenţiale (caracterizate de
amplitudinea la t = ∞, E şi constanta de timp τ). Diferite semnale elementare sunt
prezentate în figura 1.2.
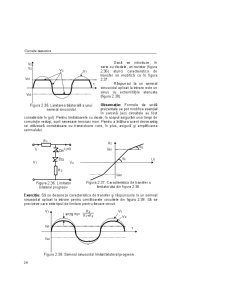
Orice semnal poate fi aşadar descompus într-o sumă de semnale
elementare. În figura 1.3. si respectiv 1.4. este prezentată descompunerea unui
semnal de tip impuls dreptunghiular, respectiv impuls trapezoidal în semnale
elementare.
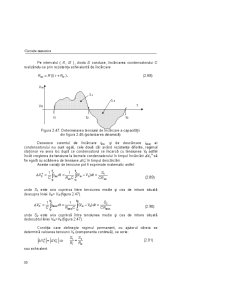
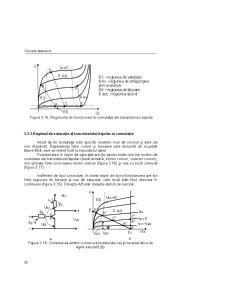
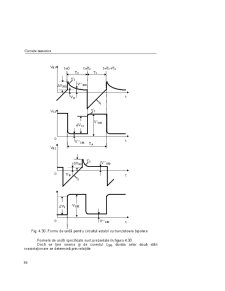
Exerciţiu: Să se descompună în semnale elementare un impuls trapezoidal cu
fronturi exponenţiale ( figura 1.5.a) şi un semnal în dinte de ferăstrău cu frontul
posterior exponenţial ( figura 1.5.b).
Fiecare din semnalele elementare pe
care le considerăm acţionează din momentul
aplicării lor până la infinit.
În cazul circuitelor de impulsuri liniare
descompunerea în semnale elementare
prezintă un interes aparte deoarece în acest
fel se poate aplica principiul superpoziţiei,
adică răspunsul global al unui circuit este
considerat ca fiind alcătuit din suma
răspunsurilor la semnalele elementare
componente.
E
ti
α1
α1
t
t
t
t
t
α2
α2
Vi1
Vi2
Vi3
Vi4
Vi
Figura 1.4. Descompunerea unui
impuls trapezoidal în semnale
elementare
Vi
E
t1 t2 Vi1
Vi2
E
t
t
t
t1
Figura 1.3. Descompunerea
unui impuls dreptunghiular în
semnale elementare
Preview document




















































































































































































Conținut arhivă zip
- Circuite Numerice.PDF
Alții au mai descărcat și
1. Prezentare generala JavaScript a fost creat de firma Netscape, ca un limbaj de programare pentru prelucrarea evenimentelor ce apar în timpul...
Introducere în programarea calculatoarelor - Circuitele electronice ale calculatoarelor sunt capabile sa efectueze un numar limitat de operaCii...
CAP. 1 SISTEME INFORMATICE 1.1 CONCEPTUL DE SISTEM INFORMATIC O firmă este sediul unor activităţi informaţionale variate (culegerea şi...
Introducere în programarea calculatoarelor 1. Utilizarea unui calculator 2. Programarea unui calculator 3. Structura şi funcţionarea unui...
Introducere. Necesitatea programării în limbaje de asamblare Modalităţile de programare s-au schimbat imens de la inventarea calculatorului, în...
Lucrarea 1 Evaluarea si masurarea timpului de executie al unui algoritm 1.Definitia unui tip de date abstract - TDA Un TDA este un model...
. Notiuni introductive Un sistem de calcul poate contine sute sau mii de componente individuale (circuite integrate, diode, rezistoare,...
1.1. Introducere în bazele de date Sistemele de baze de date pot fi considerate ca cea mai importantă realizare în domeniul ingineriei...
Te-ar putea interesa și
Definiţii Decodificatorul este un circuit digital proiectat pentru a detecta prezenţa unei stări digitale particulare. Display-ul cu 7 segmente...
Tema proiect si date tehnice Tema proiect Proiectarea unui frecventmetru numeric Caracteristicile tehnice impuse pentru proiectarea...
1.Tema proiectului Sa se proiecteze un periodmetru numeric cu urmatoarele caracteristici: - Frecventa oscilatorului 16MHz - Asfisare cu anod...
CRONOMETRUL NUMERIC Cronometrul numeric este si el tot un simplu contor de impulsuri ca si ceasul, cu diferenta ca rezolutia temporala este mai...
Introducere Circuitul de intrare ale unui aparat de masura lucreaza cu semnale analogice dar toate celelalte blocuri lucreaza cu semnale numerice....
1. Introducere Importanța măsurărilor crește necontenit în toate domeniile științei și tehnicii. Fiecare nouă cucerire a științelor naturii și a...
Proiectarea automatelor. Un mod performant de implementare a automatelor presupune utilizarea registrelor de JK-uri. Trecerea de la un automat...
Aplicatie. Să se proiecteze un automat având tranziţiile definite de diagrama de mai jos: a) cu bistabili D; b) cu bistabili JK