Teoria și Construcția Navei

Tema proiectului de curs la disciplina T.C.N.

Se dă planul de forme al unei nave având următoarele dimensiuni principale:

LCWL=120.76 m;Lmax= m; Bmax=18.03 m; T=7.50 m; D=10.52 m. Scara 1:100.

Se cer următoarele:

• întocmirea calculului de carene drepte prin metoda trapezelor de integrare aproximativă, trasarea diagramei de carene drepte, graficul funcţiei Ax=g1(x) şi trasarea scării Bonjean;

• întocmirea calculului de stabilitate la unghiuri mari de înclinare prin metoda Kîrlov-Dagnies de trasare a plutirilor şi Cebâşev de integrare şi trasare a diagramelor de stabilitate (diagrama stabilitatii statice, diagrama stabilitatii dinamice, diagrama polara a stabilitatii;

• verificarea stabilităţii navei sub acţiunea vântului pe suprafaţa velică din longitudinalul planului de forme (criteriul de vânt) după R.N.R.;

• pentru compartimentul maşini cuprins între cuplele teoretice 2 -5 şi considerate de categoria a III-a se vor efectua calculele de inundare.

CAPITOLUL 1.

ÎNTOCMIREA CALCULULUI

DE CARENE DREPTE PRIN

METODA TRAPEZELOR

Calculul de carene drepte presupune calculul si trasarea diagramelor de variaţie pentru următoarele mărimi:

a) mărimi ce se refera la plutirile drepte:

Aw =aria suprafeţei plutirii drepte;

XF= abscisa centrului geometric al plutirii drepte;

IL = moment de inerţie al suprafeţei plutirii drepte calculat fata de axa centrala longitudinala de inerţie;

IT = moment de inerţie al suprafeţei plutirii drepte calculat fata de axa centrala transversala de inerţie;

CW= coeficient de fineţe al suprafeţei plutirii.

b) mărimi ce se refera la cuplele teoretice:

AX= aria suprafeţei cuplei teoretice.

c) mărimi ce se refera la carena navei:

V = volumul carenei;

XB =abscisa centrului geometric al carenei;

KB = cota centrului geometric al carenei;

CB = coeficient de fineţe bloc al carenei;

CLP = coeficient de fineţe longitudinal prismatic;

CTP = coeficient de fineţe transversal prismatic;

CVP = coeficient de fineţe vertical prismatic.

Pentru a putea calcula si trasa graficele mărimilor de mai sus s-au extras următoarele semilatimi din planul de forme dat:

cuple: 0 1 2 3 4 5 6 7 8 9 10

p.0 -0.8 0.3 0.3 0.6 1.5 3.15 4.62 5.2 6.44 6.44 6.44

p.1 -1.1 0.45 1.12 2.89 4.5 6.35 7.58 8.32 8.7 8.7 8.7

p.2 -0.29 0.6 1.93 3.81 5.7 7.29 8.33 9 9 9 9

p.3 -2.13 0.7 2.53 4.7 6.6 7.9 8.8 9 9 9 9

p.4 -1.92 1.4 3.44 5.5 7.35 8.3 9 9 9 9 9

p.5 -2.2 2.1 4.38 6.32 7.84 8.7 9 9 9 9 9

p.6 0 4.9 5.32 7.05 8.3 8.87 9 9 9 9 9

cuple: 10 11 12 13 14 15 16 17 18 19 20

p.0 6.44 6.44 6.44 6.44 5.02 4.13 3.13 2.32 0.5 0 0

p.1 8.7 8.7 8.7 8.7 8.13 7.48 6.42 5 2.92 0.64 -1.8

p.2 9 9 9 9 9 8.29 7.36 5.88 3.83 1.47 -1.48

p.3 9 9 9 9 9 8.63 7.9 6.5 4.57 2.98 -1

p.4 9 9 9 9 9 8.84 8.12 6.89 5.02 2.4 -0.6

p.5 9 9 9 9 9 9 8.43 7.35 5.35 2.82 -0.22

p.6 9 9 9 9 9 9 8.69 7.6 5.86 3.26 0

a) Mărimi ce se refera la plutirile drepte

1.Aria suprafeţei plutirii drepte j

Se calculează cu formula:

Integrala reprezintă jumătate din aria suprafeţei plutirii drepte WjLj. Se fac următoarele ipoteze:

- se împart lungimea navei în n intervale de lungime λ= LCWL/n, utilizând în acest scop cuplele teoretice i= din planul de forme;

- toate trapezele elementare obţinute au înălţimea λ;

- laturile paralele sau bazele trapezelor elementare sunt semilăţimile yi j , i= ale navei, măsurate în planurile cuplelor teoretice i= la nivelul plutirii drepte j.

Valoarea aproximativă a integralei este dată de suma ariilor trapezelor elementare ce compun suprafaţa jumătăţii plutirii drepte. În aceste condiţii devine:

[m2]

unde j=

Plutirea de plină încărcare CWL coincide cu plutirea 5 din planul de forme.

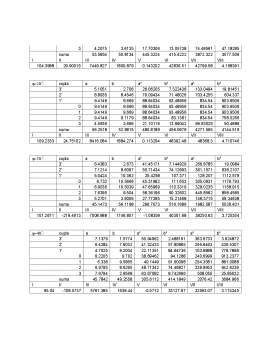
Rezultatele obtinute sunt prezentat centralizat in tabelul de mai jos: